Segment, ShapeContour and Shape
OPENRNDR offers a lot of tools for creating and drawing two dimensional shapes.
Segment
The basic element for constructing shapes is the Segment: a Bézier curve with a start point, an end point and zero, one or two control points.
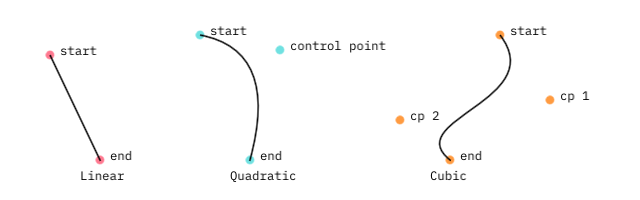
Constructing segments
// Linear Segment: start point, end point
val seg1 = Segment2D(Vector2(50.0, 55.0), Vector2(100.0, 160.0))
// Quadratic Segment: start point, control point, end point
val seg2 = Segment2D(Vector2(200.0, 35.0), Vector2(280.0, 50.0), Vector2(250.0, 160.0))
// Cubic Segment: start point, control point, control point, end point
val seg3 = Segment2D(Vector2(500.0, 35.0), Vector2(550.0, 100.0), Vector2(400.0, 120.0), Vector2(450.0, 160.0))
Drawing segments
// Draw one segment
drawer.segment(seg3)
// Draw multiple segments
drawer.segments(listOf(seg1, seg2, seg3))
Note that Segment, like Circle, Rectangle and other geometric entities in OPENRNDR, are mathematical representations which can be rendered to the screen, but this is not necessary. A reason to create such geometries without displaying them is to serve as building blocks for constructing more complex designs. We can achieve this by querying curve properties.
Segment properties
The Segment class provides multiple methods to query its properties. In the following examples, the ut argument is a normalized value that indicates a position in the segment between 0.0 (at the start) and 1.0 (at the end).
// Get a point on the curve near the start.
val pos = seg.position(ut = 0.1)
// Get the normal vector near the end.
// This is a vector of length 1.0 perpendicular to the curve.
val normal = seg.normal(ut = 0.9)
// Get the bounding box of the curve as a Rectangle instance.
val rect = seg.bounds
// Get the length of the curve.
val length = seg.length
// Get the point on the curve which is nearest to a given point.
val nearest = seg.nearest(Vector2(50.0, 50.0)).position
// Get 20 equally spaced curve points
val points = seg.equidistantPositions(20)
The list of available methods can be found at the API website or in the source code.
Modifying segments
Several methods return a new Segment based on the original one.
// Split a segment at the center returning two segments
val segments = seg.split(0.5)
// Get the center part of a segment
val subSegment = seg.sub(0.25, 0.75)
// Get the segment reversed (the start becomes the end)
val revSegment = seg.reverse
// Get the segment offset by the given distance
val offsetSegment = seg.offset(5.0)
ShapeContour
A ShapeContour is a collection of Segment instances in which each segment ends where the next one starts. A ShapeContour can be closed like the letter O or open like the letter S. It can be used to describe simple shapes like a square, or more complex ones.
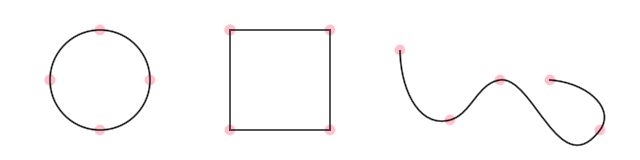
Three ShapeContours with 4 segments each. The one on the right is open.
Constructing a ShapeContour using the ContourBuilder
The ContourBuilder class offers a simple way of producing complex two dimensional shapes. It employs a vocabulary that is familiar to those who have used SVG.
moveTo(position)move the cursor to the given positionlineTo(position)insert a line contour starting from the cursor, ending at the given positionmoveOrLineTo(position)move the cursor if no cursor was previously set or draw a linecurveTo(control, position)insert a quadratic bezier curve starting from the cursor, ending at positioncurveTo(controlA, controlB, position)insert a cubic bezier curve starting from the cursor, ending at positioncontinueTo(position)inside a quadratic bezier curve starting from the cursor and reflecting the tangent of the last controlcontinueTo(controlB, position)insert a cubic splinearcTo(radiusX, radiusY, largeAngle, sweepFlag, position)close()close the contourcursoraVector2instance representing the current positionanchoraVector2instance representing the current anchor
Let’s create a simple Contour and draw it. The following program shows how to use the contour builder to create a triangular contour.

fun main() = application {
program {
extend {
val c = contour {
moveTo(Vector2(width / 2.0 - 120.0, height / 2.0 - 120.00))
// -- here `cursor` points to the end point of the previous command
lineTo(cursor + Vector2(240.0, 0.0))
lineTo(cursor + Vector2(0.0, 240.0))
lineTo(anchor)
close()
}
drawer.clear(ColorRGBa.WHITE)
drawer.fill = ColorRGBa.PINK
drawer.stroke = null
drawer.contour(c)
}
}
}
Constructing a ShapeContour from points
We can use .fromPoints() to connect points with straight segments.
The hobbyCurve method, found in orx-shapes, can be used to create smooth curves.

fun main() = application {
program {
val points = List(20) {
Vector2(20.0 + it * 32.0, 100.0 + sin(it * 1.0) * it * 3)
}
val wavyContour = ShapeContour.fromPoints(points, closed = false)
val smoothContour = hobbyCurve(points, closed = false)
extend {
drawer.clear(ColorRGBa.WHITE)
drawer.fill = null
drawer.strokeWeight = 5.0
drawer.stroke = ColorRGBa.PINK
drawer.contour(wavyContour)
drawer.translate(0.0, 10.0) // displace 10px down
drawer.stroke = ColorRGBa.BLACK.opacify(0.5)
drawer.contour(smoothContour)
}
}
}
Constructing a ShapeContour from segments
Notice how each segment starts where the last one ends.

fun main() = application {
program {
val segments = listOf(Segment2D(Vector2(10.0, 100.0), Vector2(200.0, 80.0)), // Linear Bézier Segment
Segment2D(Vector2(200.0, 80.0), Vector2(250.0, 280.0), Vector2(400.0, 80.0)), // Quadratic Bézier segment
Segment2D(Vector2(400.0, 80.0), Vector2(450.0, 180.0), Vector2(500.0, 0.0), Vector2(630.0, 80.0))) // Cubic Bézier segment
val horizontalContour = ShapeContour.fromSegments(segments, closed = false)
extend {
drawer.clear(ColorRGBa.WHITE)
drawer.strokeWeight = 5.0
drawer.stroke = ColorRGBa.PINK
drawer.contour(horizontalContour)
}
}
}
Constructing a ShapeContour from a primitive
Primitives like Rectangle, Circle and LineSegment can be easily converted into a ShapeContour.
val c1 = Circle(200.0, 200.0, 50.0).contour
Even more ways to construct a ShapeContour
Take a look at orx-turtle and orx-shapes for other ways to create contours, including regular polygons, rounded rectangles and more.
Drawing a ShapeContour
// Draw one contour
drawer.contour(contour1)
// Draw multiple contours
drawer.contours(listOf(contour1, contour2, contour3))
Note that if the contour is closed, the current fill color is used.
ShapeContour properties
The ShapeContour provides methods to query its properties similar to the ones found in Segment.
// Get a point on the contour near the start.
val pos = contour.position(ut = 0.1)
// Get the normal vector near the end.
// This is a vector of length 1.0 perpendicular to the curve.
val normal = contour.normal(ut = 0.9)
// Get the bounding box of the curve as a Rectangle instance.
val rect = contour.bounds
// Get the length of the curve.
val length = contour.length
// Get the point on the curve which is nearest to a given point.
val nearest = contour.nearest(Vector2(50.0, 50.0)).position
// Get 20 equally spaced curve points
val points = contour.equidistantPositions(20)
An example of using .position() and .equidistantPositions():
fun main() = application {
program {
extend {
drawer.clear(ColorRGBa.WHITE)
drawer.stroke = null
drawer.fill = ColorRGBa.PINK
val point = Circle(185.0, height / 2.0, 90.0).contour.position((seconds * 0.1) % 1.0)
drawer.circle(point, 10.0)
val points0 = Circle(385.0, height / 2.0, 90.0).contour.equidistantPositions(20)
drawer.circles(points0, 10.0)
val points1 = Circle(585.0, height / 2.0, 90.0).contour.equidistantPositions((cos(seconds) * 10.0 + 30.0).toInt())
drawer.circles(points1, 10.0)
}
}
}
The list of available methods can be found at the API website or in the source code.
Rectified ShapeContour
The ut argument in the ShapeContour.position() and ShapeContour.normal() methods does not specify a linear position between the start and the end of the contour.
By using rectified contours (defined in orx-shapes) we can work with evenly spaced points on contours, or animate elements traveling on a contour at the desired speed even if the contour segments vary greatly in length.
fun main() = application {
program {
val c = Pulley(Circle(Vector2.ZERO, 30.0), Circle(Vector2.ONE * 120.0, 60.0)).contour
val cr = c.rectified()
extend {
drawer.clear(ColorRGBa.WHITE)
drawer.fill = null
// Go from 0.0 to 1.0 in two seconds
// slowing down at both ends
val t = cos(kotlin.math.PI * (seconds % 2.0) / 2.0) * 0.5 + 0.5
drawer.translate(150.0, 100.0)
drawer.contour(c)
// Note how segment length affects the speed
drawer.circle(c.position(t), 5.0)
drawer.translate(270.0, 0.0)
drawer.contour(c)
// The rectified contour provides a smooth animation
drawer.circle(cr.position(t), 5.0)
}
}
}
Modifying a ShapeContour
sub()
A contour can be cut into a shorter contour using ShapeContour.sub().
fun main() = application {
program {
extend {
drawer.clear(ColorRGBa.WHITE)
drawer.fill = null
drawer.stroke = ColorRGBa.PINK
drawer.strokeWeight = 4.0
val sub0 = Circle(185.0, height / 2.0, 100.0).contour.sub(0.0, 0.5 + 0.50 * sin(seconds))
drawer.contour(sub0)
val sub1 = Circle(385.0, height / 2.0, 100.0).contour.sub(seconds * 0.1, seconds * 0.1 + 0.1)
drawer.contour(sub1)
val sub2 = Circle(585.0, height / 2.0, 100.0).contour.sub(-seconds * 0.05, seconds * 0.05 + 0.1)
drawer.contour(sub2)
}
}
}
offset()
The function ShapeContour.offset can be used to create an offset version of a contour.
fun main() = application {
program {
// -- create a contour from a Rectangle object
val c = Rectangle(100.0, 100.0, width - 200.0, height - 200.0).contour.reversed
extend {
drawer.fill = null
drawer.stroke = ColorRGBa.PINK
drawer.contour(c)
for (i in 1 until 10) {
val o = c.offset(cos(seconds + 0.5) * i * 10.0, SegmentJoin.BEVEL)
drawer.contour(o)
}
}
}
}
ShapeContour.offset can also be used to offset curved contours. The following demonstration shows a single cubic bezier offset at multiple distances.
fun main() = application {
program {
val c = contour {
moveTo(width * (1.0 / 2.0), height * (1.0 / 5.0))
curveTo(width * (1.0 / 4.0), height * (2.0 / 5.0), width * (3.0 / 4.0), height * (3.0 / 5.0), width * (2.0 / 4.0), height * (4.0 / 5.0))
}
extend {
drawer.stroke = ColorRGBa.PINK
drawer.strokeWeight = 2.0
drawer.lineJoin = LineJoin.ROUND
drawer.contour(c)
for (i in -8..8) {
val o = c.offset(i * 10.0 * cos(seconds + 0.5))
drawer.contour(o)
}
}
}
}
reversed, close(), transform(), …
For more properties and methods explore the API website or the source code.
Shape
OPENRNDR uses Shape to represent planar shapes. We can think of a Shape as a group of ShapeContour instances, where each ShapeContour is a sequence of one or more Bézier Segment.
Constructing a Shape using the shape builder
Let’s create a Shape using the shape builder. The shape is created using two contours, one for the outline of the shape, and one for the hole in the shape

fun main() = application {
program {
extend {
val s = shape {
contour {
moveTo(Vector2(width / 2.0 - 120.0, height / 2.0 - 120.00))
lineTo(cursor + Vector2(240.0, 0.0))
lineTo(cursor + Vector2(0.0, 240.0))
lineTo(anchor)
close()
}
contour {
moveTo(Vector2(width / 2.0 - 80.0, height / 2.0 - 100.0))
lineTo(cursor + Vector2(190.0, 0.0))
lineTo(cursor + Vector2(0.0, 190.00))
lineTo(anchor)
close()
}
}
drawer.clear(ColorRGBa.WHITE)
drawer.fill = ColorRGBa.PINK
drawer.stroke = null
drawer.shape(s)
}
}
}
Constructing a Shape from a primitive
Primitives like Rectangle, Circle, LineSegment and ShapeContour can be easily converted into a Shape.
val s = Circle(200.0, 200.0, 50.0).shape
Shape Boolean-operations
Boolean-operations can be performed on shapes using the compound {} builder. There are three kinds of compounds: union, difference and intersection, all three of them are shown in the example below.
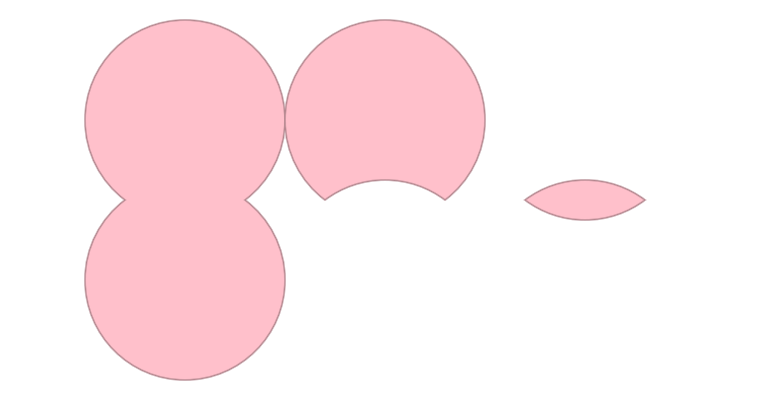
fun main() = application {
program {
extend {
drawer.clear(ColorRGBa.WHITE)
drawer.fill = ColorRGBa.PINK
drawer.stroke = ColorRGBa.PINK.shade(0.7)
// -- shape union
val su = compound {
union {
shape(Circle(185.0, height / 2.0 - 80.0, 100.0).shape)
shape(Circle(185.0, height / 2.0 + 80.0, 100.0).shape)
}
}
drawer.shapes(su)
// -- shape difference
val sd = compound {
difference {
shape(Circle(385.0, height / 2.0 - 80.0, 100.0).shape)
shape(Circle(385.0, height / 2.0 + 80.0, 100.0).shape)
}
}
drawer.shapes(sd)
// -- shape intersection
val si = compound {
intersection {
shape(Circle(585.0, height / 2.0 - 80.0, 100.0).shape)
shape(Circle(585.0, height / 2.0 + 80.0, 100.0).shape)
}
}
drawer.shapes(si)
}
}
}
The compound builder is actually a bit more clever than what the previous example demonstrated because it can actually work with an entire tree of compounds. Demonstrated below is the union of two intersections.

fun main() = application {
program {
extend {
drawer.clear(ColorRGBa.WHITE)
drawer.fill = ColorRGBa.PINK
drawer.stroke = ColorRGBa.PINK.shade(0.7)
val cross = compound {
union {
intersection {
shape(Circle(width / 2.0 - 160.0, height / 2.0, 200.0).shape)
shape(Circle(width / 2.0 + 160.0, height / 2.0, 200.0).shape)
}
intersection {
shape(Circle(width / 2.0, height / 2.0 - 160.0, 200.0).shape)
shape(Circle(width / 2.0, height / 2.0 + 160.0, 200.0).shape)
}
}
}
drawer.shapes(cross)
}
}
}
Intersections
Extension methods are provided to find intersections between Shape, ShapeContour and Segment instances.
fun main() = application {
program {
extend {
// A rotation transformation to apply to the rectangle
val rotation = transform {
translate(width * 0.6, height * 0.5)
rotate(seconds * 18)
}
val circle = Circle(width * 0.4, height * 0.5, 80.0).contour
val rotatingRect = Rectangle.fromCenter(Vector2.ZERO, 150.0).contour.transform(rotation)
val intersections = circle.intersections(rotatingRect)
drawer.clear(ColorRGBa.WHITE)
drawer.strokeWeight = 2.0
drawer.stroke = ColorRGBa.PINK
drawer.fill = ColorRGBa.PINK.opacify(0.5)
drawer.contour(circle)
drawer.contour(rotatingRect)
// Draw intersections as small circles
drawer.fill = ColorRGBa.WHITE
drawer.stroke = ColorRGBa.BLACK.opacify(0.5)
drawer.circles(intersections.map {
it.position
}, 5.0)
}
}
}